数理逻辑期末复习整理

Table of Contents

• 绪论
• 形式化公理系统
• 命题逻辑的基本概念
• 命题与联结词
• 范式
• 联结词的扩充与规约
• 对偶式
• 命题演算形式系统
• 命题演算形式系统
• 自然演绎推理系统
• 一阶谓词逻辑演算基本概念
• 一阶谓词逻辑演算的基本概念
• 一阶谓词逻辑形式系统
• 一阶谓词演算形式系统组成
• FC 的基本定理

绪论

形式化公理系统

数理逻辑形式系统的组成

​ （1）用于将概念符号化的语言，通常为一形式语言，包括符号表$\Sigma$及语言的文法，可生成对象的语言成分项，表示概念、判断的公式。

​ （2）表示思维规律的逻辑学公理模式和推理规则模式（抽象的形式公理系统），及依据它们推演出的全部定理组成的理论体系。

形式语言

​ （1）字符串是由字母表中的字符构成的有限长的序列

​ （2）字符串的子集称为形式语言

​ （3）可以用有限状态自动机来表示其可接受的字符串集合

命题逻辑的基本概念

命题与联结词

命题

​ （1）定义：能判断真假的陈述句

​ （2）原子命题：不包含其他命题成分的命题称为原子命题

​ （3）复合命题：至少包含一个其他成分的命题称为复合命题

​ （4）支命题：组成复合命题的那些命题称为支命题

命题联结词及真值表

​ （1）最基本、最常用的 5 个逻辑联结词：$\land（合取词）, \lor（析取词）, \rightarrow（蕴含词）, \leftrightarrow（双条件词）, \rightharpoondown（否定词）$

​ （2）真值表

$p$	$q$	$\rightharpoondown p$	$p \land q$	$p \lor q$	$p\rightarrow q$	$p\leftrightarrow q$
0	0	1	0	0	1	1
0	1	1	0	1	1	0
1	0	0	0	1	0	0
1	1	0	1	1	1	1

命题公式及真值

​ （1）定义：由命题常元、命题变元及逻辑联结词复合而成的表达式称为命题公式

​ （2）原子命题就是命题公式

​ （3）若 A, B 是命题公式，则$\rightharpoondown A,A\lor B, A \land B, A \rightarrow B, A \leftrightarrow B$均是命题公式

​ （4）指派：对公式$A(p_1, p_2, ..., p_n)$中的 n 个命题变元$p_1, p_2, p_3, ..., p_n$的任意一种真值赋值称为指派

​ （5）若公式 A 含有 n 个命题变元， 则共有$2^n$个不同的指派

​ （6）根据公式的真值取值情况的不同，可以将公式分为三类：

​ i 重言式（永真式）： 任一真值指派均为真

​ ii 永假式： 任一真值指派均为假

​ iii 可满足式： 若公式 A 存在一个指派使其真值为真，则称为可满足式

​ 考试可能会考永真式的判定，判断的方法有三种，分别是：真值表，计算方法，反证法

​ 命题公式的计算：

​ $(\rightharpoondown A)^v = 1 - A^v$ $(A\land B)^v = A^v \cdot B^v$ $(A\lor B)^v = A^v + B^v - A^v \cdot B^v$

​ $(A\rightarrow B)^v = 1-A^v + A^v\cdot B^v$ $(A\leftrightarrow B)^v = A^v\cdot B^v + (1-A^v)(1-B^v)$

逻辑蕴含与逻辑等价

​ （1）逻辑蕴含：对公式$A, B$，如果所有弄真 A 的指派也弄真公式 B，则称 A 逻辑蕴含 B

​ （2）逻辑等价：公式 A,B 逻辑等价当且仅当$A\Rightarrow B 且 B\Rightarrow A$记为$A\Leftrightarrow B$

​ （3）等价关系：

​ i 自反: 对任意的$A\in Form(L^p)$都有$A\Leftrightarrow A$

​ ii 对称：对任意$A, B\in Form(L^p)$, 若$A \Leftrightarrow B$, 则$B \Leftrightarrow A$

​ iii 传递：对任意$A, B.C\in Form(L^p)$, 若$A \Leftrightarrow B, B\Leftrightarrow C$, 则$A \Leftrightarrow C$

​ 常见的逻辑等价式：

​ 对合律： $\rightharpoondown\rightharpoondown A \Leftrightarrow A$ 幂等律：$A\land A \Leftrightarrow A$ $A \Leftrightarrow A \land A$ 交换律： $A\land B \Leftrightarrow B \land A$ $B \land A \Leftrightarrow A$

​ 结合律： $(A\land B)\land C \Leftrightarrow A \land (B\land C)$ 分配律： $A\land (B\lor C) \Leftrightarrow (A\lor B)\land(A\lor C)$

​ 析取律： $A\land(A\lor B) \Leftrightarrow A$ 德摩根律： $\rightharpoondown (A \lor B) \Leftrightarrow \rightharpoondown A \land \rightharpoondown B$

​ 同一律： $A\land 1 \Leftrightarrow A$ 零一律：$A\land 0 \Leftrightarrow 0$

​ （4）替换定理：设 C 为命题公式 A 中的子命题公式，若$C\Leftrightarrow D$则将 C 用 D 替换（未必对所有的子公式 C 作替换）后得到公式 B，满足$A \Leftrightarrow B$

​ （5）代入定理：设 A 为含命题变元 p 的重言式，则将 A 中 p 的所有出现均替换为命题公式 B，所得的公式仍为重言式

范式

范式

​ （1）定义：命题公式 B 称为命题公式 A 的合取（析取）范式，如果$B \Leftrightarrow A$, 并且 B 呈如下形式$C_1\land C2 \land C3 \land ... \land C_m$($C_1 \lor C_2 \lor C_3 \lor ... \lor Cm$)其中$C_i$称为B的子句，它们形如$L_1 \lor L_2 \lor L_3 \lor .. \lor L_n$($L_1 \land L_2 \land L_3 \land ... \land L_n$)，$L_i$称为原子公式

​ （2）范式定理：对任意公式$\phi$，都可以作出相应的析取范式与合取范式

​ i 消去蕴含与等价：$A\to B \Leftrightarrow \rightharpoondown A \lor B$ $A \leftrightarrow B \Leftrightarrow (A\land B)\lor (\rightharpoondown A \land \rightharpoondown B)$

​ ii 减少否定词的辖域：利用德摩根定律

​ iii 主次使用合取对析取，析取对合取满足分配率将公式化成合取或析取范式

​ iv 析取范式和合取范式的并不唯一

主范式

​ （1）定义：命题公式 B 称为命题公式 A 的主合取（析取）范式，如果

​ i B 是 A 的合取（析取）范式

​ ii B 中的每一个子句均出现 A 中所有命题变元且只出现一次

​ iii 主合取范式是以极大项为子句的合取范式，主析取范式是以极小项为子句的析取范式

​ （2）主析取范式和主合取范式的求解步骤：

​ 方法一：首选真值表法，具体方法与数字逻辑中的逻辑表达式化简相同

​ 方法二：i 求解命题公式的合取（析取）范式

​ ii 除去合取（析取）范式中所有永真永假项

​ iii 合并相同变元与相同的项

​ iv 对合取（析取）项中缺少的变元 r，通过析取（合取）永假式（永真式）$r\land \rightharpoondown r$

​ （$r\lor \rightharpoondown r$）并用分配率补齐

弄假指派与范式

​ （1）命题 1：对于一个命题公式的任何一个指派，这个指派可以弄假一个子句，这个子句包含命题公式中的所有命题变元且只包含一次，在这类子句中，这个指派不能弄假任何其他的子句，从而弄真所有其他的子句

​ （2）命题 2：对于一个公式的任何一个弄假指派，则有该命题公式的一个主合取范式中的一个合取项，使得这一个指派弄假这个合取项，并且只弄假这个合取项

​ （3）命题 3：通过公式的主合取范式可以直接写出公式的弄假指派，这就是公式的所有弄假指派。

​ （4）命题 4：如果已知公式的所有弄假指派，可以写出该公式的主合取范式

​ （5）命题 5：如果已知公式的所有弄真指派，可以写出该公式的主析取范式

​ （6）定理 1：永真式无主合取范式，永假式无主析取范式

​ （7）定理 2：任意命题公式都存在与之唯一对应的主析取范式和主合取范式

​ （8）定理 3：极大项和极小项的全体数目之和为$2^n$

联结词的扩充与规约

n 元联结词的个数

​ （1）n 元命题公式的全体可以划分为$2^{2^n}$个等价类，每一类中的公式相互逻辑等价，都等价于它们的主合取范式（主析取范式）

一元联结词

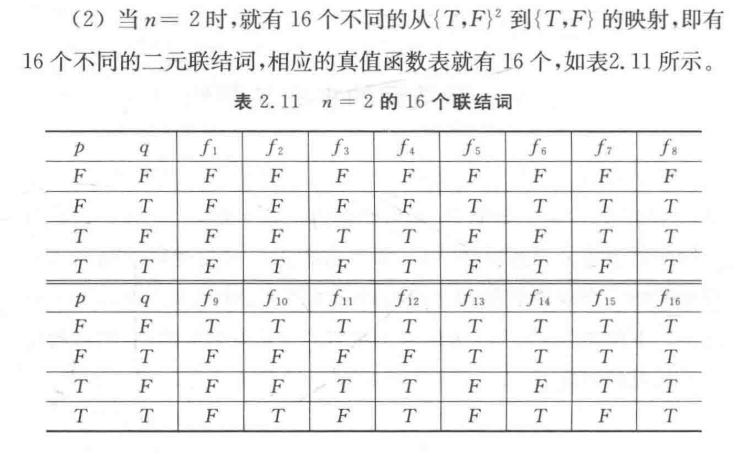
二元联结词

联结词的表示与完备词组

​ （1）联结词的可表示：设 h 为一 n 元联结词，A 为由 m 个联结词$g_1, g_2, .., g_m$（联结词组）构成的命题公式，若有$h(p_1, p_2, p_3,...,p_n)\Leftrightarrow A$，则称可由联结词$g_1, g_2, ...,g_m$来表示

​ （2）联结词的完备集：设 C 为联结词的集合，若对任意一个命题公式都可以由 C 中的联结词表示出来的公式与之对应，则称 C 是联结词的完备集，或称 C 是完备的联结词集合

​ （3）$\{\rightharpoondown, \land, \lor\}$是完备的联结词集合 （证明采用数学归纳法进行证明）

​ （4）联结词完备集还有或非词$\{\uparrow\}$, 与非词$\{\downarrow\}$ $p\uparrow q \Leftrightarrow \rightharpoondown (p\lor q)$ $p \downarrow q \Leftrightarrow \rightharpoondown(p \land q)$

​ （5）联结词完备集还有$\{\rightharpoondown, \lor\}$, $\{\rightharpoondown, \land\}$ , $\{\rightharpoondown, \to\}$

对偶式

​ （1）定义：仅含有联结词$\rightharpoondown, \lor, \land$的命题公式 A 中，将$\lor$换成$\land$， 将$\land$换成$\lor$， F 换成 T， T 换成 F，得到的公式称为 A 的对偶式，记为$A^*$

​ （2）内否式：设有命题公式$A(p_1, p_2,..., p_n)$，对 A 中的$p_i(i = 1, 2, 3, ..., n)$用$\rightharpoondown p_i$做代入的结果为 A 的内否式， 记为$A^-$

​ （3）$(A^*)^* \Leftrightarrow A$ , $(A^-)^- \Leftrightarrow A$ , $\rightharpoondown (A^*) \Leftrightarrow (\rightharpoondown A^*) \Leftrightarrow A^-$ , $\rightharpoondown A \Leftrightarrow (A^*)^-$ , $\rightharpoondown (A^-) \Leftrightarrow(\rightharpoondown A)^-$ , $(\rightharpoondown A)^- \Leftrightarrow A^*$

​ （4）若$A \Leftrightarrow B$永真， 则$A^* \Leftrightarrow B^*$

​ （5）若$A\to B$永真， 则$B^*\to A^*$也永真

命题演算形式系统

命题演算形式系统

命题演算形式系统的组成

​ （1）语言部分：PC 的字符集 $\Sigma = \{(, ), \to, \rightharpoondown, p, q, r, p_1, p_2, p_3, ...\}$, PC 中的公式$p, q, r, p_1, p_2, p_3,...$为原子公式，如果 A， B 是公式， 那么$(\rightharpoondown A), (A\to B)$也是公式

​ （2）推理规则

​ i 公理集合： $A_1: A \to(B \to A)$ $A_2: (A\to (B\to C))\to ((A\to B)\to (A\to C))$

​ $A_3: (\rightharpoondown A \to \rightharpoondown B)\rightarrow(B \to A)$

​ ii 推理规则： 称为分离规则， 形式如下：$r_{mp} = \frac{A, A\to B}{B}$

命题演算形式系统的基本定理

​ （1）证明：称下列公式序列为公式 A 在 PC 中的一个证明：$A_1, A_2, ..., A_m(=A)$， 如果对任意的$i\in\{1, 2, 3,...,m\}$， $A_i$或者是 PC 中的公理， 或者是$A_j(j<i)$或者是$A_j, A_k(j<k<i)$用分离规则导出的，其中$A_m$就是公式 A

​ （2）定理：称 A 是 PC 中的定理， 记为$\vdash_{PC} A$，如果公式 A 在 PC 中有一个证明

​ （3）演绎：设$\Gamma$为 PC 公式的集合，称以下公式序列为公式 A 的一个以$\Gamma$为前提，在 PC 中的演绎：$A_1,A_2, ..., A_m(=A)$其中$A_i$或者是 PC 中的公理， 或者是$\Gamma$中的成员， 或者是$A_j(j<i)$或者是$A_j, A_k(j<k<i)$用分离规则导出的，其中$A_m$就是公式 A

​ （4）演绎结果：称 A 是前提$\Gamma$在 PC 中的演绎结果， 记为$\Gamma \vdash_{PC}A$, 如果公式 A 有一个以$\Gamma$为前提在 PC 中的演绎， 如果$\Gamma = B$则用$B\vdash_{PC}A$表示$\Gamma\vdash_{PC}A$如果$B\vdash A$且$A\vdash B$则记为$A\vdash\dashv B$

基本定理

​ （1）定理 1： $\vdash A\to A$

​ （2）定理 2：如果$\vdash A(B\to C)$ 那么$\vdash B\to(A\to C)$

​ （3）前件后换定理 3：$\vdash(A\to(B\to C))\to(B\to(A\to C))$

​ （4）加前件定理 4：$\vdash(B\to C)\to ((A\to B)\to(A\to C))$

​ （5）加后件定理 5：$\vdash(A\to B)\to ((B\to C)\to (A\to C))$

​ （6）定理 6：$\vdash \rightharpoondown A\to(A\to B)$

​ （7）定理 7：$\vdash A\to(\rightharpoondown A \to B)$

​ （8）三段论定理 8：如果$\vdash(A\to B)$ $\vdash(B\to C)$那么$\vdash(A\to C)$

​ （9）定理 9：$\vdash(\rightharpoondown A\to A)\to A$

​ （10）定理 10：$\rightharpoondown \rightharpoondown A \to A$

​ （11）定理 11：$\vdash (A\to \rightharpoondown A)\to \rightharpoondown A$

​ （12）定理 12：$\vdash A\to \rightharpoondown\rightharpoondown A$

​ （13）逆否定理 13：$\vdash(A\to B)\to(\rightharpoondown B\to \rightharpoondown A)$

​ （14）定理 14：$\vdash(\rightharpoondown A\to B)\to (\rightharpoondown B \to A)$

​ （15）定理 15：$\vdash(A\to \rightharpoondown B)\to (B\to \rightharpoondown A)$

​ （16）定理 16：$\vdash(\rightharpoondown A\to B)\to ((\rightharpoondown A\to \rightharpoondown B)\to A)$

​ （17）定理 17：$\vdash(A\to B)\to ((A\to \rightharpoondown B)\to \rightharpoondown A)$

​ （18）定理 17.5：如果$\vdash \rightharpoondown A\to C$并且$\vdash B\to C$则$\vdash(A\to B)\to C$

​ （19）定理 17.6：如果$\vdash(A\to B)\to C$ 那么$\vdash \rightharpoondown A\to C$并且 $B\to C$

​ （20）定理 18：$A\to A\lor B$， 其中$A\lor B$定义为$\rightharpoondown A \to B$

​ （21）定理 19：$A\to B\lor A$

​ （22）定理 20：$\vdash(A\to C)\to ((B\to C)\to ((A\lor B)\to C))$

​ （23）定理 21：$\vdash\rightharpoondown(A\to \rightharpoondown B)\to C$当且仅当 $\vdash(A\to B)\to C$

​ （24）定理 22：如果$\vdash P\to Q, \vdash R\to S$ 那么$\vdash(Q\to R)\to (P\to S)$

​ （25）定理 23：$\vdash A\land B\to C$当且仅当 $\vdash A\to (B\to C)$其中$A\land B \Leftrightarrow \rightharpoondown (A\to \rightharpoondown B)$

​ （26）定理 24：$\vdash A\land B \to A$

​ （27）定理 25：$\vdash A\land B\to B$

​ （28）定理 26：$\vdash A\to (B\to A\land B)$

​ （29）定理 27：$\vdash(A\to B)\to ((A\to C)\to(A\to B\land C))$

​ （30）定理 28：$\vdash A\lor B \leftrightarrow B\lor A$

​ （31）定理 29：$\vdash A\land B \leftrightarrow B\land A$

​ （32）定理 30：$\vdash (A\lor B)\lor C \leftrightarrow A\lor(B\lor C)$

​ （33）定理 31：$\vdash (A\land B)\land C \leftrightarrow A\land(B\land C)$

​ （34）定理 32：$\vdash A\land(A\lor B)\leftrightarrow A$

​ （35）定理 33：$\vdash A\lor (A \land B)\leftrightarrow A$

​ （36）定理 34：$\vdash A\land (B\lor C)\leftrightarrow (A\land B)\lor (A\land C)$

​ （37）定理 35：$\vdash A\lor(B\land C)\leftrightarrow (A\land B)\lor(A\land C)$

PC 基本定理

​ （1）演绎定理：对 PC 中人任意公式集合$\Gamma$和公式 A,B， $\Gamma\cup\{A\}\vdash_{PC}B$当且仅当$\Gamma \vdash_{PC}A\to B$

​ （2）PC 的合理性:PC 是合理的，即对任意公式集$\Gamma$和公式 A，如果$\Gamma\vdash A$，则$\Gamma \Rightarrow A$。特别是如果 A 是 PC 中的一个定理，则 A 永真

​ （3）公式集的一致性：设$\Gamma$是 PC 的一个公式集，如果不存在 PC 的公式 A，使得$\Gamma\vdash A$与$\Gamma\vdash \rightharpoondown A$同时成立，则称$\Gamma$是一个一致的公式集

​ （4）公式集的完全性：设$\Gamma$是 PC 的一个公式集，如果对任一的公式 A，$\Gamma\vdash A$或者$\Gamma\vdash \rightharpoondown A$必有一个成立，则称$\Gamma$是一个完全的公式集

​ （5）PC 的一致性：PC 是一致的，即不存在公式 A，使得 A 与$\rightharpoondown A$均是 PC 中的定理

​ （6）PC 的不完全性：PC 不是完全的，即存在公式 A，使得$\vdash A, \vdash\rightharpoondown A$均不能成立

​ （7）PC 的理论：PC 的理论指如下的集合：$Th(PC)=\{A|\vdash_{pc}A\}$, 称集合$Th(PC\cup\Gamma)=\{A|\Gamma \vdash_{PC}A\}$为 PC 基于前提$\Gamma$的扩充

​ （8）不一致性与完全性

​ （9）完备性定理

​ （10）公式集的一致性和可满足性

PC 的证明常用方法

​ （1）利用前件互换定理： $(A\rightarrow(B\rightarrow C)) \rightarrow (B\rightarrow(A\rightarrow C))$

​ （2）利用传递规律及其变形

​ 构造中间件来进一步推演：

​ i 有相同尾件的时候考虑加前件定理四： $(B\rightarrow C)->((A\rightarrow B)\rightarrow (A\rightarrow C))$

​ ii 有相同前件的时候考虑加后件定理五或者公理 2：$(A\rightarrow B)\rightarrow ((B\rightarrow C)\rightarrow (A\rightarrow C))$

​ iii 有的时候尾件相同不好处理，或者一个尾件与另一个前件相反时可以通过逆否的形式变化转化

​ 为前件相同来处理

​ （3）利用前提不一致可以证明任何结论： 往往是倒推的最后一步，开始证明的第一步

​ （4）利用定理 7.5 要证明$(A\rightarrow B)\rightarrow C$ 等价于证明 $(\rightharpoondown A \rightarrow C)$与$B \rightarrow C$

​ （5）利用演绎定理，极大简化运算

自然演绎推理系统

自然演义推理系统的组成

​ （1）语言部分：语言部分与 PC 系统的语言部分相似，ND 知识将联结词由完备集$\{\rightharpoondown, \to\}$ 扩充到$\{\rightharpoondown, \land, \lor, \to, \leftrightarrow\}$

​ （2）推理部分（公理）：$\Gamma \cup\{A\}\vdash A(\in)$

​ （3）推理规则

​ 推理规则 1：假设引入规则

​ $\frac{\Gamma\vdash B}{\Gamma;A\vdash B}$ 出自重言式 $B\to(A\to B)$

​ 推理规则 2：假设消除规则

​ $\frac{\Gamma ; A \vdash B ; \Gamma ; \neg A \vdash B}{\Gamma \vdash B}$ 出自重言式$\neg \mathrm{A} \rightarrow(\mathrm{A} \rightarrow \mathrm{B}))$

​ 推理规则 3：$\lor$引入规则

​ $\frac{\Gamma \vdash A}{\Gamma \vdash A \vee B}, \frac{\Gamma \vdash A}{\Gamma \vdash B \vee A}$ 出自重言式$\mathrm{A} \rightarrow \mathrm{A} \vee \mathrm{B}, \mathrm{B} \rightarrow \mathrm{A} \vee \mathrm{B}$

​ 推理规则 4：$\lor$消除规则

​ $\frac{\Gamma ; A \vdash C, \Gamma ; B \vdash C, \Gamma \vdash A \vee B}{\Gamma \vdash C}$ 出自重言式$(\mathrm{A} \vee \mathrm{B}) \wedge(\mathrm{A} \rightarrow \mathrm{C}) \wedge(\mathrm{B} \rightarrow \mathrm{C}) \rightarrow \mathrm{C}$

​ 推理规则 5：$\land$引入规则

​ $\frac{\Gamma \vdash A, \Gamma \vdash B}{\Gamma \vdash A \wedge B}$ 出自重言式$\mathrm{A} \rightarrow(\mathrm{B} \rightarrow \mathrm{A} \wedge \mathrm{B})$

​ 推理规则 6：$\land$消除规则

​ $\frac{\Gamma \vdash A \wedge B}{\Gamma \vdash A}, \frac{\Gamma \vdash A \wedge B}{\Gamma \vdash B}$ 出自重言式$\mathrm{A} \wedge \mathrm{B} \rightarrow \mathrm{A}, \mathrm{A} \wedge \mathrm{B} \rightarrow \mathrm{B}$

​ 推理规则 7：$\to$引入原则

​ $\frac{\Gamma ; A \vdash B}{\Gamma \vdash A \rightarrow B}$

​ 推理规则 8：$\to$消除原则

​ $\frac{\Gamma \vdash A, \Gamma \vdash A \rightarrow B}{\Gamma \vdash B}$

​ 推理规则 9：$\rightharpoondown$引入原则

​ $\frac{\Gamma ; A \vdash B, \Gamma ; A \vdash \neg B}{\Gamma \vdash \neg A}$

​ 推理规则 10：$\rightharpoondown$消除规则

​ $\frac{\Gamma \vdash A, \Gamma \vdash \rightarrow}{\Gamma \vdash B}$ 出自重言式$A\to(\neg A\to B)$

​ 推理规则 11：$\rightharpoondown\rightharpoondown$引入规则

​ $\frac{\Gamma \vdash A}{\Gamma \vdash \neg \neg A}$

​ 推理规则 12：$\rightharpoondown\rightharpoondown$消除规则

​ $\frac{\Gamma \vdash \neg \neg A}{\Gamma \vdash A}$

​ 推理规则 13：$\leftrightarrow$引入规则

​ $\frac{\Gamma \vdash A \rightarrow B, \Gamma \vdash B \rightarrow A}{\Gamma \vdash A \leftrightarrow B}$

​ 推理规则 14：$\leftrightarrow$消除规则

​ $\frac{\Gamma \vdash A \leftrightarrow B}{\Gamma \vdash A \rightarrow B}, \frac{\Gamma \vdash A \leftrightarrow B}{\Gamma \vdash B \rightarrow A}$

自然演义推理系统的基本定理

​ （1）演绎结果 在 ND 中称 A 为$\Gamma$的演绎结果，记为$\Gamma \vdash_{ND}A$，如果存在一个序列$\Gamma_{1}\vdash A_1, \Gamma_2\vdash A_2, ..., \Gamma_m\vdash A_m(=\Gamma\vdash A)$,使得对任意的$i=1, 2, 3,...,m$ $\Gamma_i\vdash A_i$或者公理，或者是$\Gamma_j\vdash A_j(j<i)$，或者是$\Gamma_{j1}\vdash A_{j1}, \Gamma_{j2}\vdash A_{j2}, ..., \Gamma_{jm}\vdash A_{jm}$使用推理规则导出。称 A 为 ND 的定理，如果 Γ ⊢ A，并且 Γ = ϕ。即 ⊢ A

​ （2）$\vdash A\lor \rightharpoondown A$

​ （3）$\vdash\neg(A\lor B)\leftrightarrow\neg A \land \neg B$

​ （4）$\vdash\neg(A\land B) \leftrightarrow (\neg A\land \neg B)$

​ （5）$\neg A\to B\vdash \dashv A\lor B$

​ （6）$A\to B\vdash\dashv \neg A\lor B$

​ （7）$\vdash\mathrm{A} \wedge(\mathrm{B} \vee \mathrm{C}) \leftrightarrow(\mathrm{A} \wedge \mathrm{B}) \vee(\mathrm{A} \wedge \mathrm{C}) \vdash \mathrm{A} \vee(\mathrm{B} \wedge \mathrm{C}) \leftrightarrow(\mathrm{A} \vee \mathrm{B}) \wedge(\mathrm{A} \vee \mathrm{C})$

​ （8）PC 的公理是 ND 的定理

ND 证明的常用方法

​ （1）思考要引入什么，决定下一个方向

​ （2）$\lor$在条件中常常需要考虑$\lor$的消除： 在条件有$A\lor B$的时候，在条件中加入 A 或者加入条件 B 若都能推导出结果 C，则原条件能推出结果 C

​ （3）$\lor$在结果的时候常常考虑假设消除：在结果有$A\lor B$的时候，在条件加入 C 或者$\rightharpoondown C$都能推出 A 或者 B 其中一个，那么原条件可以推出结果$A\lor B$

​ （4）没有什么思路的时候就加条件，考虑假设消除或者**$\rightharpoondown$的消除**规则

一阶谓词逻辑演算基本概念

一阶谓词逻辑演算的基本概念

​ （1）个体词：用于表示研究对象的词，分为个体常元与个体变元

​ （2）谓词：表示研究对象的性质或研究对象直接关系的词称为谓词

​ （3）n 元谓词：含有 n 个命题变元的谓词称为 n 元谓词。仅含有一个个体变元的谓词称为一元谓词

​ （4）个体域个体变元的取值范围称为个体域，用$D$来表示

​ （5）函词：用于描述从一个个体域到另一个个体域的映射

​ （6）量词：用于限制个体词的数量，分为全称量词和存在量词

​ i 全称量词（$\forall$）表示任意的，从量上表示“所有的”

​ ii 存在量词（$\exists$）表示存在，从量上表示“至少有一个”

​ （7）项：个体常元、个体变元是项； 若$f^{(n)}$是一个 n 元函词，且$t_1, t_2, ..., t_n$是项，则$f^{(n)}(t_1, t_2, t_3, ..., t_n)$是项； 由前两个有限次符合产生的结果是项

​ （8）合式公式

​ i 不含联结词的单个谓词即原子谓词公式是合式公式

​ ii 若 A 为合式公式，则$\neg A$也是合式公式

​ iii 若 A，B 为合式公式，且无变元 x 在 A，B 中是一个约束的，而在另一个是自由的，则$A\lor B, A\land B, A\to B, A\leftrightarrow B$都是合式公式

​ iv 若 A 是合式公式，而 x 在 A 中为自由变元，则$\forall xP(x),\exists xP(x)$均是合式公式

​ v 由 i~iv 有限次复合所形成的的公式均为合式公式

​ （9）变元

​ i 约束变元: 受量词约束的个体变元称为约束变元

​ ii 自由变元：不受两次约束的个体变元

​ （10）辖域：量词所约束的范围

​ （11）易名规则：将量词辖域中出现的某个约束变元改成另一个在该辖域中未出现的个体变元，工事中的其余部分保持不变。改名后的公式称为原公式的改名式，注意所有变元应均被改掉

自然语言的形式化

一阶谓词逻辑形式系统

一阶谓词演算形式系统组成

一阶语言

​ （1）字符集

​ i 个体变元：$x,y,z,u,v,w,...$

​ ii 个体常元： $a, b, c, d, e$

​ iii n 元函词：$f^{(n)},g^{(n)}, h^{(n)}, ...$

​ iv n 元谓词：$P^{(n)}, Q^{(n)}, R^{(n)}, ...$

​ v 真值联结词：$\rightharpoondown, \to$

​ vi 量词：$\forall$

​ vii 技术型括号：（， ）

​ （2）形成规则 由基本字符集形成项和谓词公式的定义

​ i $L(FC)$的项： 变元和常元是项； 对任意正整数 n，如果$t_1, t_2, t_3, ..., t_n$为项， $f^{(n)}$为 n 元函词，那么$f^{(n)}(t_1, t_2, ..., t_n)$也是项； 除了有限次使用上述得到的表达式外，其余的都不是项

​ ii $L(FC)$的公式：对任意正整数 n，如果$t_1, t_2, ..., t_n$为项，$P^{(n)}$为 n 元谓词符号，那么$P^{(n)}(t_1, t_2, t_3, ..., t_n)$也是公式，并称之为原子公式； 如果 A， B 为公式， v 为任意一个变元符号，那么$\neg A$, $A\to B$, $\forall vA$都是公式； 除了有限次使用上述表达式以外的其他表达式均不是公式

公理和推理规则

​ （1）公理模式，由下列公式及所有的全程化组成

​ $AX_{1.1}: A \to(B \to A)$

​ $AX_{1.2}: (A\to (B\to C))\to ((A\to B)\to (A\to C))$

​ $AX_{1.3}: (\rightharpoondown A \to \rightharpoondown B)\rightarrow(B \to A)$

​ $AX_2:\forall vA\to A^v_t$ 含义：t 对 A 中的变元 v 可代入

​ $AX_3:\forall v(A\to B)\to(\forall vA\to \forall vB)$

​ $AX_4:A\to \forall vA$ (v 在 A 中无自由出现)

​ （2）推理规则： 称为分离规则， 形式如下：$r_{mp} = \frac{A, A\to B}{B}$

FC 的基本定理

​ （1）定理 1：对于 FC 中的任何公式 A， 变元 v，$\vdash_{FC}\forall vA\to A$

​ （2）定理 2：对于 FC 中的任何公式 A， 变元 v， $\vdash_{FC}A\to \neg \forall v\neg A$

​ （3）定理 3：对于 FC 中的任何公式 A， 变元 v， $\vdash_{FC}\forall vA\to \exists vA$

​ （4）全称推广定理 4：对于 FC 中的任何公式 A，变元 v，如果$\vdash A$, 那么$\vdash\forall vA$

​ （5）定理 5：对于 FC 中的任何公式集合$\Gamma$，公式 A，以及不在$\Gamma$的任意公式里自由出现的变元 v，如果$\Gamma\vdash A$，那么$\Gamma \vdash \forall vA$

​ （6）演绎定理 6：设$\Gamma$为 FC 中任一公式集合，A，B 为 FC 中任意两个公式，那么$\Gamma;A\vdash B$当且仅当$\Gamma \vdash A \to B$

​ （7）定理 7：设$\Gamma$为任一公式集合，A，B 为 FC 中任意两个公式，那么$\Gamma;A\vdash \neg B$当且仅当$\Gamma;B \vdash \neg A$

​ （8）反证法定理 8：如果 FC 中的公式集合$\Gamma\cup\{A\}$是不一致的，那么$\Gamma\vdash\neg A$

​ （9）定理 9：设$\Gamma$为 GC 中任一公式集合，A，B 为 FC 中任意两个公式，并且变元 v 不在$\Gamma$的任何公式里面自由出现，那么$\Gamma;A\vdash B$蕴含$\Gamma ; \forall vA \vdash B$和$\Gamma ; \forall vA \vdash \forall vB$

​ （10）存在消除定理 10：设 Γ 为 FC 中的任一公式集合， A,B 为 FC 中的任意两个公式，并且变元 v 不在 Γ 的任何公式以及公式 B 里面自由出现，那么由 Γ ⊢ ∃vA 以及 Γ;A ⊢ B 可以推出 Γ ⊢ B

​ （11）替换定理 11：设 A,B 为 FC 的公式，且满足 A ⊢ ⊣ B （即 A ⊢ B 且 B ⊢ A ），A 是 C 的子公式， D 是将 C 中 A 的若干出现换为公式 B 得到的公式，则 C ⊢ ⊣ D

​ （12）改名定理 12：在 FC 中，若 A′是 A 的改名式，且 A′改用的变元不在 A 中出现， 则 A ⊢ ⊣ A′

​ （13）定理 13：$\exists \mathrm{x} \neg \mathrm{A} \vdash \dashv \neg \forall \mathrm{xA}$ $\forall \mathrm{x} \neg \mathrm{A} \vdash \dashv \neg \exists \mathrm{xA}$

​ （14）定理 14：$\forall x (A \land B)\vdash \dashv \forall xA\land \forall xB$ $\exists x(A\land B)\vdash \dashv\exists xA \land \exists x B$

​ （15）定理 15： $\exists x(A\lor B)\vdash \exists xA \lor \exists x B$ $\forall xA\lor \forall xB \vdash \forall x(A\lor B)$ $\exists x \forall y B(x,y)\vdash \forall y \exists x B(x, y)$

FC 的证明常用方法

​ （1）FC 的演绎定理

​ （2）$\forall vA\to A \to \exists vA$这一连串变化始终成立，但是$A\to \forall vA$只有在 v 在 A 中无自由出现时才成立

​ （3）逆着思考的时候常常利用全称推广去掉最外面的那一层$\forall$，然后再思考证明那个式子

​ （4）条件中有存在什么式子的时候考虑存在消除